| Introduction |
|---|
| Features |
| Download/ Installation |
| Documentation |
| Tutorial |
| Change Log |
Generating a parallel surface
A parallel surface or an offset surface if you prefer is a surface for which the points on one surface are equidistant to a corresponding point in another one and the derivative at that point is the same on both surfaces. I'll admit my library doesn't currently ensure that a resulting parallel surface will behave exactly like this, but it's close enough.
The algorithm computes the points for the parallel surface such that s(u,v) is defined from a generating surface as s(u,v) + d * n(u,v), where s(u,v) is the point on the surface, d is the distance between them and n(u,v) is the normal at the point (u,v).
The library cuts corners by only moving the points associated with the control points: the points of maximal influence. It doesn't verify that the relationship between the two surfaces holds for all (u,v). If you'd prefer to have a more robust implementation, talk to me.
Remember when using this function that the parallel surface is generated by using the normal to the surface. If the surface as a normal which is mis-behaving you will get strange results. It doesn't happen often, so you shouldn't loose sleep over this.
An example with the nurbs editor
-
Generate a NURBS surface by creating a plane. Select generate:surface:Basic Shape then accept the default for a plane and click on 'Ok'.
-
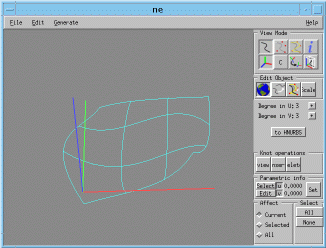
Move some of the control points to have a more interesting surface. You can end up with a surface which looks like the following figure.
-
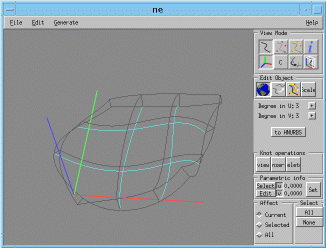
Generate a parallel surface by selecting generate:surface:by Offsetting. Accept the default, click 'Ok' and you end up with something like this
Notice that with the default values the sides surfaces are also generated to create a volume. Also, the default value of 0.1 generates a surface which is below the generating surface. If you move the object in 3D you will notice that every line is parallel to it's neighbour, for instance all the side surface have a 90 degree angle.